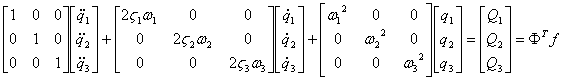機械力学演習１２月１９日

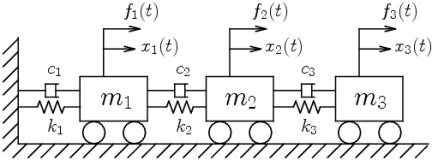
１． 機械運動系において、質量が外力を受け、直線運動を生ずる。このとき、次の設問に答えよ。

1) マトリクス運動方程式を求めよ（すでに先週求めているので、その結果を書く）。

2) 外力と減衰力が零の同次運動方程式において、固有振動解析を行い、固有振動数と振動モードを求めよ。ここで、

, N/m Ns/mは、学生番号の数字で最下位桁とその上位の値から、

m1 ｍ2=ｍ3 ｋ1 ｋ2=ｋ3

０　→　1.5 2.5 1500 1000

１　→　2.0 3.0 2000 1500

２　→　2.5 3.5 2500 2000

３　→　3.0 4.0 3000 2500

４　→　3.5 4.5 3500 3000

５　→　4.0 5.0 4000 3500

６　→　4.5 5.5 4500 4000

７　→　5.0 6.0 5000 4500

８　→　5.5 6.5 5500 5000　　　　　　　　図　３自由度直動振動系

９　→　6.0 7.0 6000 5500

とする。例えば、04T1026Rは、ｍ1＝4.5 kg, m2=m3=5.5 kg, k1=2500 N/m, k2=k3=2000N/m である。また

減衰マトリクスは剛性マトリクスの0.1倍()の値、外力項はf=[1 0 0]’とする。

ここで、マトリクス運動方程式は教科書の正規化

を使い、[V,E]=eig(A)を使って固有振動数と振動モードを計算せよ。なお、A: 行列、V: 各列が固有ベクトルの固有マトリクス、E: 固有値が対角要素に並んだマトリクスである。
3) 固有ベクトルをもとの変数ｘに関する固有マトリクス =inv(sqrt(m))*V に戻し、これを使って ’*m*が単位マトリクスに、’*ｋ*が周波数マトリクスに、’*ｃ*が減衰マトリクスになることを確かめよ。ただし、である。
4) 上記の変換は、マトリクス運動方程式
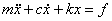が対角変換によって、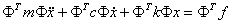のモード領域の運動方程式が得られる。これを求め、マトリクス運動方程式を


の形に表示せよ。注意：固有値解析プログラム[V,E]=eig(A)の固有値解Eと対応するベクトルVは、必ずしも小さい順には並ばない。大きさの順番（固有値解の番号）は適切に判断するように！